判断链表是否有环
问题
链表有环是指链表中“最后”的一个节点,它的下一个节点指向了链表中位于它之前的节点。
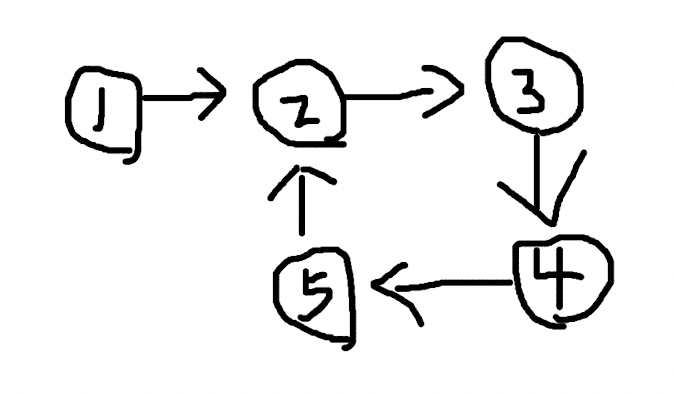
当程序遍历这个链表,会发现进入了死循环,永远找不到出口了。怎么判断一个链表,是否存在这样的环呢?
分析
常用的解决思路是双指针。设想一个在赛道上的场景,两个人 A 和 B 处于同样的起点,但是他们跑步的速度并不相同,A 的速度 v1=1,B 的速度 v2=2,也就是 B 比 A 快。在这样的情况下,只要他们不停,B 一定会超过 A 一圈然后再次追上 A,这是一种生活中的常识。
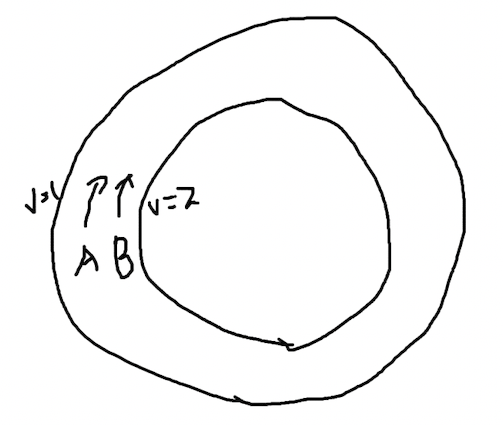
在一个圈里,一快一慢的两个点一定会再次相遇,而且他们经过的路程是可以计算的,路程 s1 和 s2 应该满足这样的关系:
s2 - s1 = nR
R 是圆圈的周长,n 是正整数,他们位于出发点时 n=0,第一次相遇的时候 B 比 A 多跑了一圈,多出了 1 倍周长的路程,n=1。
和链表的情景相比较,赛道的场景还少了开始的一段距离,在进入赛道之前,A 和 B 会先从赛道外的小路进入赛道,然后再开始绕圈跑步。他们的起点在赛道外,为了便于计算,他们的速度从始至终不发生变化,那么当他们进入赛道之后,就已经不是同样的起点了。
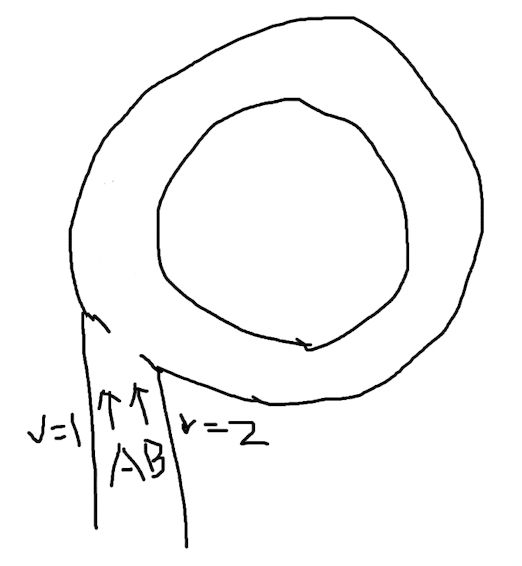
在这种情况下,他们经过的路程 s1 和 s2 还有规律可循吗?设圆形赛道外的直道距离为 d,相比上面的关系式,他们在圆圈内的路径依然满足 n 倍的周长 R,只不过现在的表达式不同了:
(s2 - d) - (s1 - d) = nR
s2 - d - s1 + d = nR
s2 - s1 = nR
结果表达式在相互抵消路径 d 之后,和之前的一样。
A 的路程 s1=v1t,B的路程 s2=v2t,时间 t 是一样的,速度 v1 和 v2 是已知的 1 和 2,有:
s2 - s1 = nR
v2t - v1t = nR
2t - t = nR
t = nR
取 n = 1,t = R。
解决
回到链表的问题,其实我们只要用快慢指针就可以判断链表是否有环了,并不需要知道他们具体相遇的点在哪儿,不过计算路径关系的公式可以辅助我们验证结果的正确性。
回到这个链表,用两个指针 A 和 B 从节点 1 分别以速度 1 和 2 出发:

他们的位置关系将会是:
| 时间 t | 0 | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| A 的位置 | 节点 1 | 节点 2 | 节点 3 | 节点 4 | 节点 5 |
| B 的位置 | 节点 1 | 节点 3 | 节点 5 | 节点 3 | 节点 5 |
在第 4 个时间点的时候,A 和 B 相遇了,环的周长正好等于 4,满足 t = R 的关系。